.../Структура/ЛДО

Предложены новые эффективные методы расчёта элементов неизображающей оптики, формирующих заданные распределения освещённости. Методы основаны на формулировке задачи неизображающей оптики как задачи о перемещении масс с различными функциями стоимости и последующем сведении данной задачи к линейной задаче о назначениях.
Предложенный подход был разработан и применён к расчёту следующих элементов неизображающей оптики:

• Зеркало, формирующее заданное распределение освещённости в дальнем поле в случае точечного источника света.
• Преломляющий элемент, формирующий заданное распределение освещённости в дальнем поле в случае коллимированного источника света.
• Преломляющий элемент, формирующий заданное распределение освещённости в дальнем поле в случае точечного источника света.
• Преломляющий элемент, формирующий заданное распределение освещённости в ближнем поле в случае коллимированного источника света.
• Преломляющий элемент с двумя поверхностными свободной формы, преобразующий коллимированнй пучок в коллимированный c заданным распределением освещённости.

Предложенный метод важен при решении задач интерьерного и дорожного освещения, а также при разработке светотехнических устройств автомобилей.

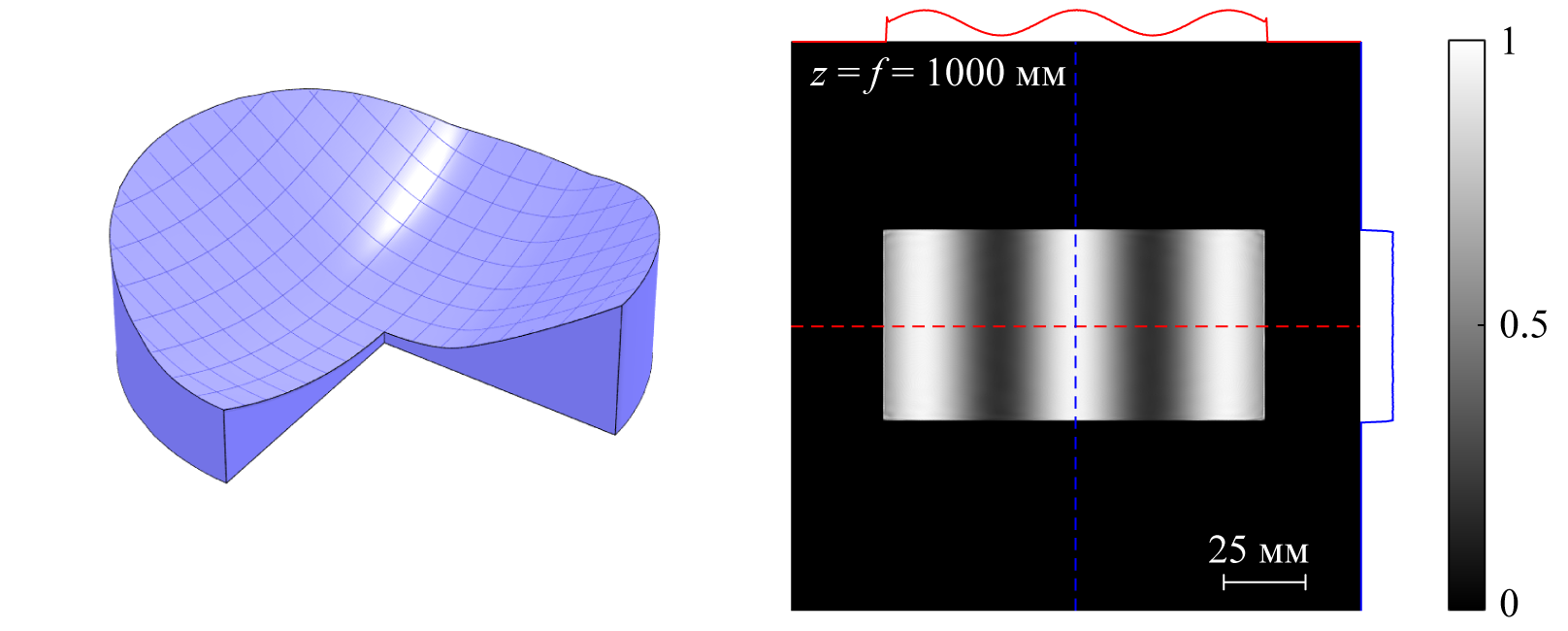
Рассчитанный преломляющий элемент (слева), формирующий из коллимированного пучка заданное распределение освещённости в дальнем поле (справа)

Рассчитанный преломляющий элемент (слева), формирующий из точечного источника заданное распределение освещённости в дальнем поле (справа)

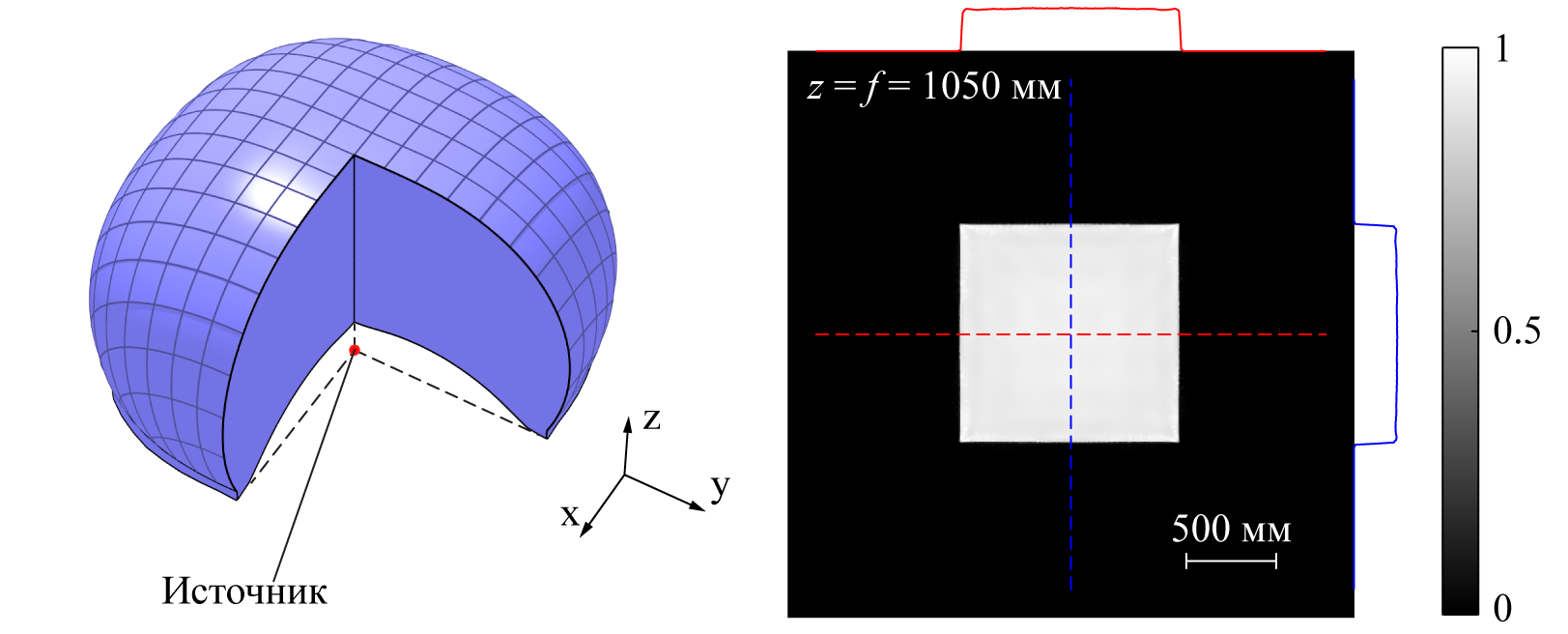
Рассчитанное зеркало (слева), формирующее из точечного источника заданное распределение освещённости в дальнем поле (справа)

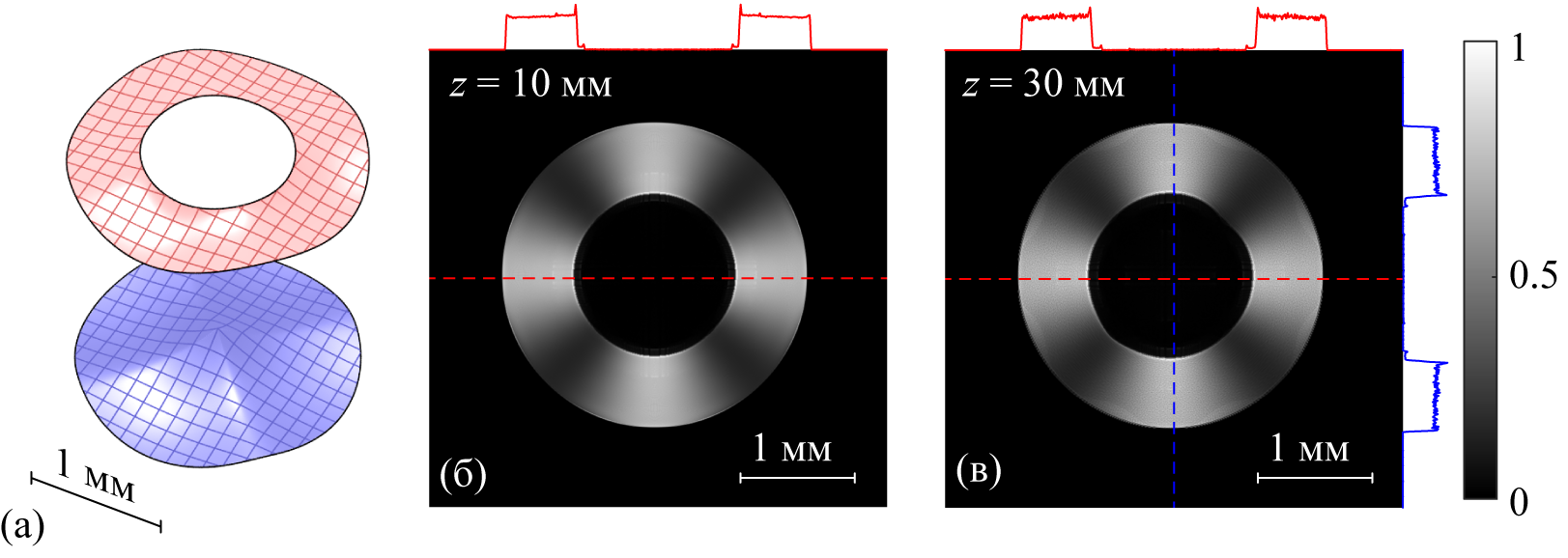
Рассчитанная пара преломляющих поверхностей (слева), формирующая из коллимированного пучка круглого сечения коллимированный пучок с заданным распределение освещённости (справа)

Публикации:

1. D. A. Bykov, L. L. Doskolovich, and E. A. Bezus, “Multiscale approach and linear assignment problem in designing mirrors generating far-field irradiance distributions”, Optics Letters 13, 3549–3552 (2020).
2. A. I. Mingazov, D. A. Bykov, E. A. Bezus, and L. L. Doskolovich, “On the use of the supporting quadric method in the problem of designing double freeform surfaces for collimated beam shaping”, Optics Express 28, 22642–22657 (2020).
3. L. L. Doskolovich, D. A. Bykov, E. S. Andreev, E. V. Byzov, M. A. Moiseev et al., “Design and fabrication of freeform mirrors generating prescribed far-field irradiance distributions”, Applied Optics 59, 5006–5012 (2020).
4. L. L. Doskolovich, D. A. Bykov, A. A. Mingazov, and E. A. Bezus, “Optimal mass transportation and linear assignment problems in the design of freeform refractive optical elements generating far-field irradiance distributions”, Optics Express 27, 13083–13097 (2019).
5. D. A. Bykov, L. L. Doskolovich, A. A. Mingazov, and E. A. Bezus, “Optimal mass transportation problem in the design of freeform optical elements generating far-field irradiance distributions for plane incident beam”, Applied Optics 58, 9131–9140 (2019).
6. D. A. Bykov, L. L. Doskolovich, A. A. Mingazov, E. A. Bezus, and N. L. Kazanskiy, “Linear assignment problem in the design of freeform refractive optical elements generating prescribed irradiance distributions”, Optics Express 26, 27812–27825 (2018).
7. L. L. Doskolovich, D. A. Bykov, E. S. Andreev, E. A. Bezus, and V. Oliker, “Designing double freeform surfaces for collimated beam shaping with optimal mass transportation and linear assignment problems”, Optics Express 26, 24602–24613 (2018).
8. V. Oliker, L. L. Doskolovich, and D. A. Bykov, “Beam shaping with a plano-freeform lens pair”, Optics Express 26, 19406–19419 (2018).
9. L. L. Doskolovich, A. A. Mingazov, D. A. Bykov, E. S. Andreev, and E. A. Bezus, “Variational approach to calculation of light field eikonal function for illuminating a prescribed region”, Optics Express 25, 26378–26392 (2017).