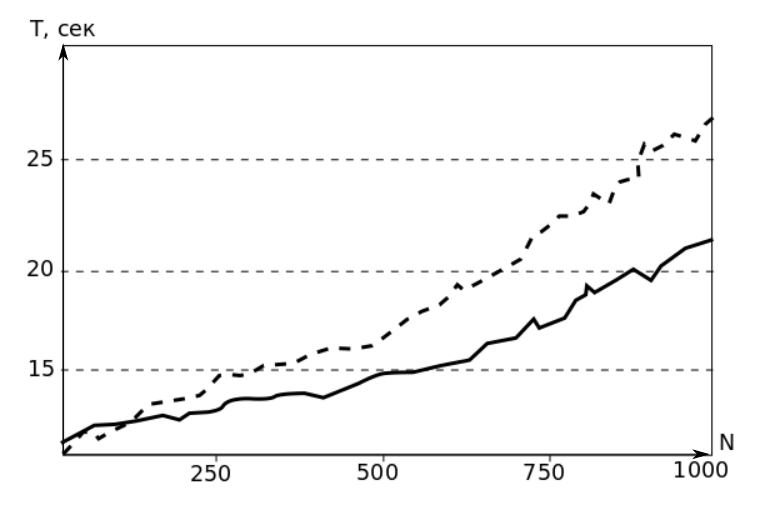
Сравнение длительности вычислений по B-CALM (прерывистая линия) и новому длинновекторныму алгоритму (сплошная)
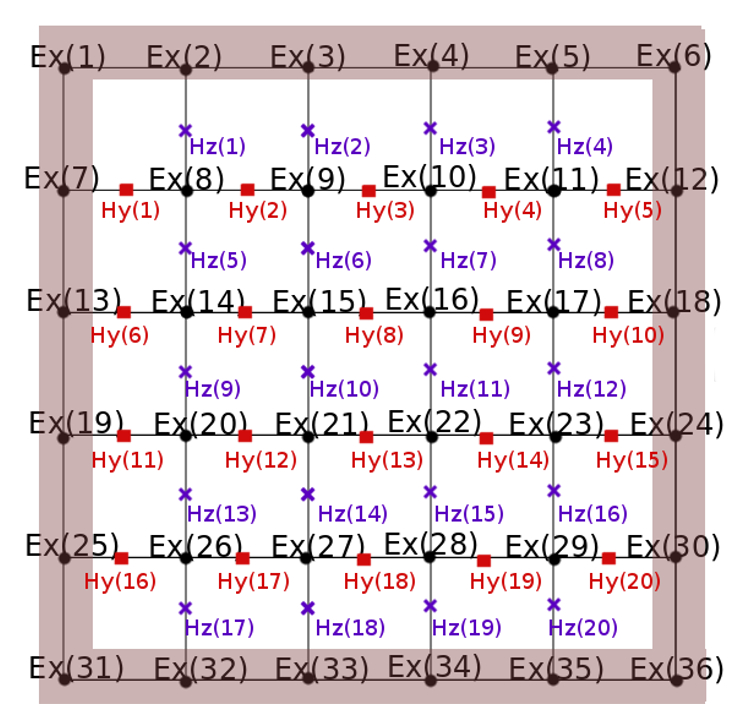
Ускорение вычислений при разностном решении уравнений дифракционной оптики
1. Разработан численный метод решения сеточных уравнений явных разностных схем, основанный на использовании векторов с длиной, равной количеству узлов сеточной области и ориентированный на производство векторных вычислений на графических процессорах. Реализация векторного алгоритма, основанного на операции gaxpy, позволила добиться ускорения вычислений (от 1,2 до 1,4 раз в диапазоне от 250 до 1000 тысячи узлов сеточной области по одному пространственному направлению) при разностном решении уравнений Максвелла по сравнению с пакетом B-CALM Калифорнийского технологического института.
 |
 |
| Предложенное правило формирования векторов на двумерной сеточной области | Сравнение длительности вычислений по B-CALM (прерывистая линия) и новому длинновекторныму алгоритму (сплошная) |
2. Разработан численный метод совместного разностного решения волнового уравнения и системы уравнений Максвелла, характеризующийся по сравнению с FDTD-методом сокращением на четверть объема используемой памяти ЭВМ и в 2,6 раза длительности вычислений. Последний результат практически не зависит от марки процессора серии Intel Core (сравнивались Intel Core i3, i5 и i7), версии операционной системы Linux (сравнивались Ubuntu и CentOS), компилятора (использовались gfortran, PGI Fortran и Intel Fortran) и совпадает с разработанной теоретической оценкой, основанной на сравнении коммуникаций между оперативной памятью ЭВМ и кэш-памятью процессора в ходе расчетов по двум упомянутым методам. Выдвинуто и подтверждено предположение о решающем влиянии указанных коммуникаций на общую длительность расчетов, практически не зависящую от вычислительной сложности алгоритмов решения явных сеточных уравнений.
процессор |
операционная система и компилятор |
алгоритмы и пакеты |
||
MEEP+PML |
FDTD+PML |
JS+PML |
||
i7-3770 |
Ubuntu и GCC |
122,68 |
109,16 |
42,43 |
Cent OS и PGI Fortran |
|
108,53 |
43,18 |
|
i5-4200M |
Ubuntu и GCC |
206,40 |
173,60 |
66,09 |
Ubuntu и Intel Fortran |
|
173,56 |
65,96 |
|
i3-4150 |
Ubuntu и GCC |
186,2 |
157,99 |
59,79 |
Сравнение длительности вычислений (в секундах) для пакета MEEP разработки Массачусетского технологического университета, FDTD - программы Susan C. Hagness, прилагающейся к текстам фундаментальных монографий Allen’а Taflove и JS – совместного разностного решения
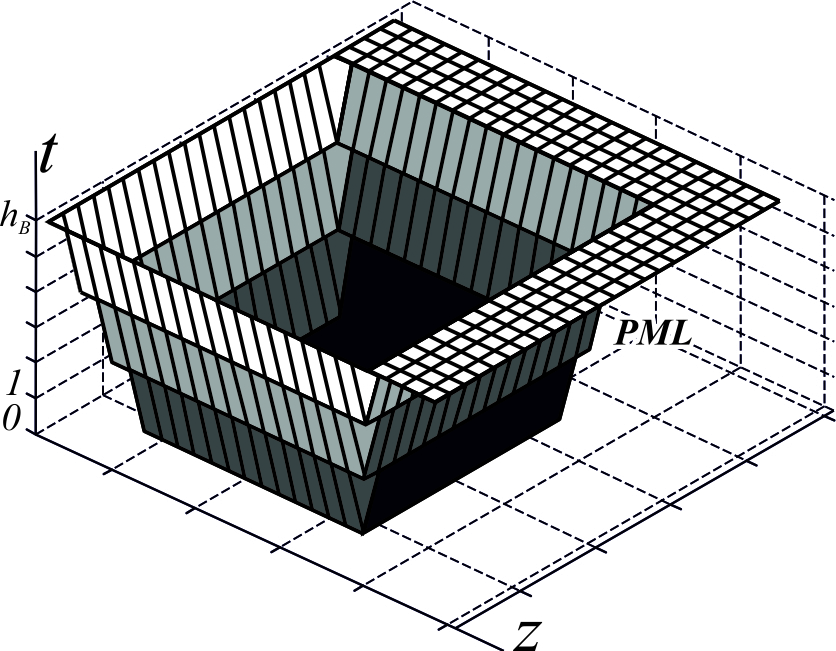
3. Синтезированы блочные алгоритмы совместного разностного решения волнового уравнения и уравнений Максвелла, отличающиеся от традиционного подхода к решению сеточных уравнений (послойное нахождение значений сеточных функций) переходом к другому порядку вычислений на пространстве итераций, связанному с производством расчетов внутри локальной подобласти (блока), пересекающей несколько временных слоев сеточной области. Найдена форма блока, обеспечивающая наилучшее ускорение вычислений по сравнению тривиальным подходом. На упомянутой ранее аппаратной и системой базе оно достигало 1,9 раза по отношению к не блочной реализации авторского численного метода и 5,88 и 4,99 раз по сравнению с программными реализациями Массачусетского технологического университета и Susan C. Hagness соответственно. Сформулирована и подтверждена теоретическая оценка размера блока, обеспечивающего наименьшую длительность расчетов, связанная с ёмкостью уровня кэш-памяти L3 процессора.
 |
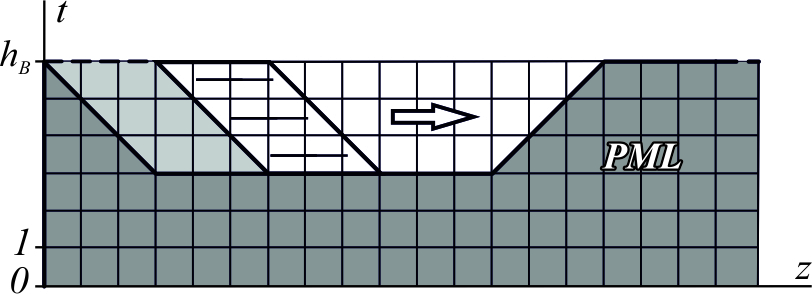 |
| Распределение найденных значений сеточных функций по временным слоям перед началом блочного этапа вычислений. От белого (слои на максимальной высоте hB и рядом) к черному (слои на минимальной высоте и около нее). Под ручкой ковша расположены PML-слои | Распределение найденных значений сеточных функций по временным слоям на блочном этапе вычислений. Темно-серый цвет – значения функций, определенные до блочного этапа, светло-серый – уже определены в его ходе, внутри выделенного параллелограмма - вычисляются на настоящий момент, белый – ожидают определения. |
Публикации: