.../Структура/ЛДО
Резонансные структуры нанофотоники для аналоговых оптических вычислений
Исследованы временные, пространственные и пространственно-временные преобразования оптических пучков и импульсов, реализуемые резонансными структурами нанофотоники. В частности, показано, что резонансные дифракционные решётки позволяют дифференцировать и интегрировать оптические импульсы. Показано, что пространственные преобразования, реализуемые резонансными дифракционными решётками и брэгговскими решётками с дефектом, включают вычисление первой и второй производных, интеграла и оператора Лапласа. Описан общий вид пространственно-временных преобразований, реализуемых указанными структурами. Частными случаями общих преобразований являются операции дифференцирования и интегрирования по временным и пространственным переменным.
Практическая значимость результата состоит в возможности создания новых систем сверхбыстрой оптической обработки информации и оптических вычислений (в частности, для оптического решения дифференциальных уравнений в частных производных эллиптического и параболического типов), а также в возможности создания новых оптических элементов для преобразования формы оптических пучков и импульсов.
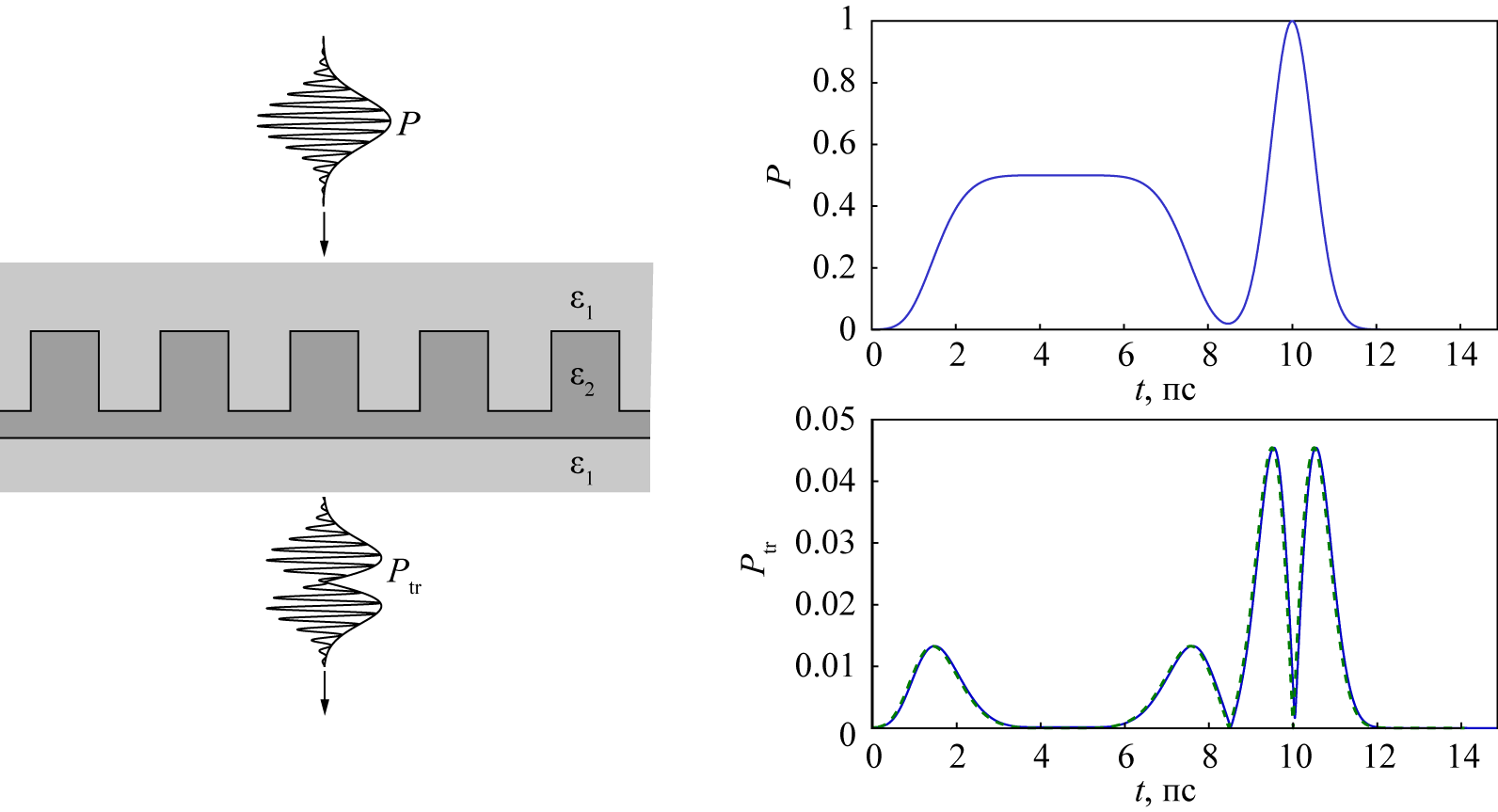
Слева: дифракция оптического импульса на резонансной дифракционной решётке. Справа: огибающая падающего импульса. (сверху); огибающая прошедшего импульса (непрерывная линия снизу) и модуль аналитически вычисленной производной от огибающей падающего импульса (пунктир).
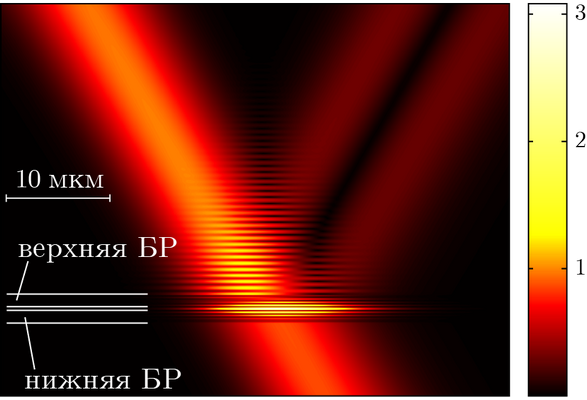
Вычисление первой производной: дифракция наклонно падающего двумерного пучка на брэгговской решётке с дефектом.
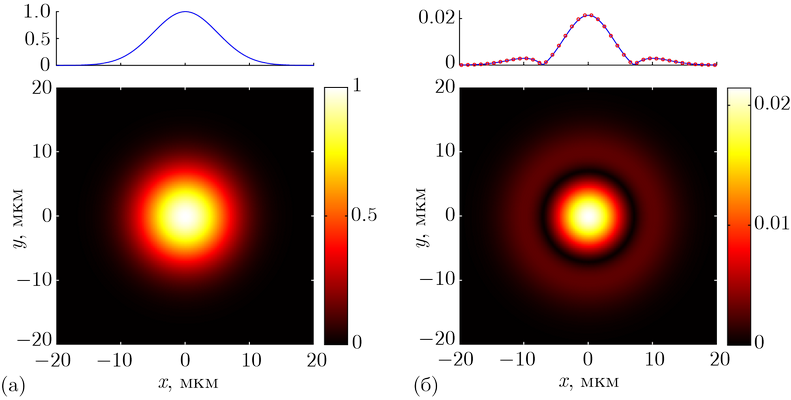
Вычисление оператора Лапласа брэгговской решёткой с дефектом: модуль огибающей падающего пучка (а) и прошедшего пучка (б). Сверху показаны сечения, полученные в результате численного моделирования. Кружочками показаны предсказания, полученные на основе аналитической модели.
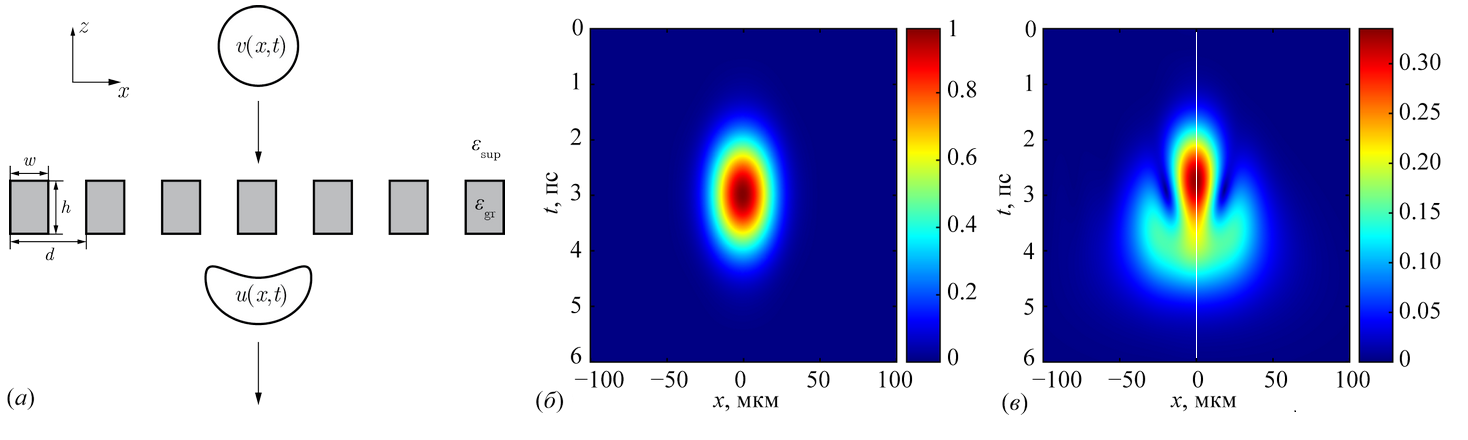
Дифракция импульса на резонансной дифракционной решётке (a). Модуль огибающей импульса: (б) падающий импульс, (в) прошедший импульс (левая часть вычислена строго по методу Фурье-мод, правая часть получена с использованием предложенной аналитической модели).
Публикации:
- D. A. Bykov, L. L. Dokolovich, A. A. Morozov, V. V. Podlipnov, E. A. Bezus, et al., “First-order optical spatial differentiator based on a guided-mode resonant grating”, Optics Express 26, 10997–11006 (2018).
- E. A. Bezus, L. L. Doskolovich, D. A. Bykov, and Soifer. V. A., “Spatial integration and differentiation of optical beams in a slab waveguide by a dielectric ridge supporting high-Q resonances”, Optics Express 26, 25156–25165 (2018).
- L. L. Doskolovich, E. A. Bezus, N. V. Golovastikov, D. A. Bykov, and V. A. Soifer, “Planar two-groove optical differentiator in a slab waveguide”, Optics Express 25, 22328–22340 (2017).
- N. V. Golovastikov, D. A. Bykov, L. L. Doskolovich, and V. A. Soifer, “Analytical description of 3D optical pulse diffraction by a phase-shifted Bragg grating”, Optics Express 24, 18828–18842 (2016).
- L. L. Doskolovich, E. A. Bezus, D. A. Bykov, and V. A. Soifer, “Spatial differentiation of Bloch surface wave beams using an on-chip phase-shifted Bragg grating”, Journal of Optics 18, 115006 (2016).
- N. V. Golovastikov, D. A. Bykov, and L. L. Doskolovich, “Spatiotemporal pulse shaping using resonant diffraction gratings”, Optics Letters 40, 3492–3495 (2015).
- Н. В. Головастиков, Д. А. Быков, Л. Л. Досколович и В. А. Сойфер, “Преобразование пространственно-временного оптического импульса резонансной дифракционной решёткой”, ЖЭТФ 148, 899–907 (2015).
- N. V. Golovastikov, D. A. Bykov, L. L. Doskolovich, and E. A. Bezus, “Spatial optical integrator based on phase-shifted Bragg gratings”, Optics Communications 338, 457–460 (2015).
- L. L. Doskolovich, D. A. Bykov, E. A. Bezus, and V. A. Soifer, “Spatial differentiation of optical beams using phase-shifted Bragg grating”, Optics Letters 39, 1278–1281 (2014).
- D. A. Bykov, L. L. Doskolovich, E. A. Bezus, and V. A. Soifer, “Optical computation of the Laplace operator using phase-shifted Bragg grating”, Optics Express 22, 25084–25092 (2014).
- D. A. Bykov, L. L. Doskolovich, N. V. Golovastikov, and V. A. Soifer, “Time-domain differentiation of optical pulses in reflection and in transmission using the same resonant grating”, Journal of Optics 15, 105703 (2013).
- D. A. Bykov, L. L. Doskolovich, and V. A. Soifer, “Single-resonance diffraction gratings for time-domain pulse transformations: integration of optical signals”, J. Opt. Soc. Am. A 29, 1734–1740 (2012).
- Д. А. Быков, Л. Л. Досколович и В. А. Сойфер, “Интегрирование оптических импульсов резонансными дифракционными решетками”, Письма в ЖЭТФ 95, 8–12 (2012).
- Д. А. Быков, Л. Л. Досколович и В. А. Сойфер, “О способности резонансных дифракционных решеток дифференцировать импульсный оптический сигнал”, ЖЭТФ 141, 832–839 (2012).
- D. A. Bykov, L. L. Doskolovich, and V. A. Soifer, “Temporal differentiation of optical signals using resonant gratings”, Optics Letters 36, 3509–3511 (2011).



