СВЕРХБЫСТРЫЕ
АЛГОРИТМЫ
ДИСКРЕТНЫХ ОРТОГОНАЛЬНЫХ ПРЕОБРАЗОВАНИЙ
И ПАРАЛЛЕЛЬНО-РЕКУРСИВНОГО ВЫЧИСЛЕНИЯ СВЕРТОК
Новые алгоритмы вычисления
ДПФ основаны на комбинированном использовании известных схем редукции (Кули-Тьюки,
Гуда-Томаса, Винограда) в сочетании со специальным представлением данных
в рекуррентных системах счисления в полях алгебраических чисел.
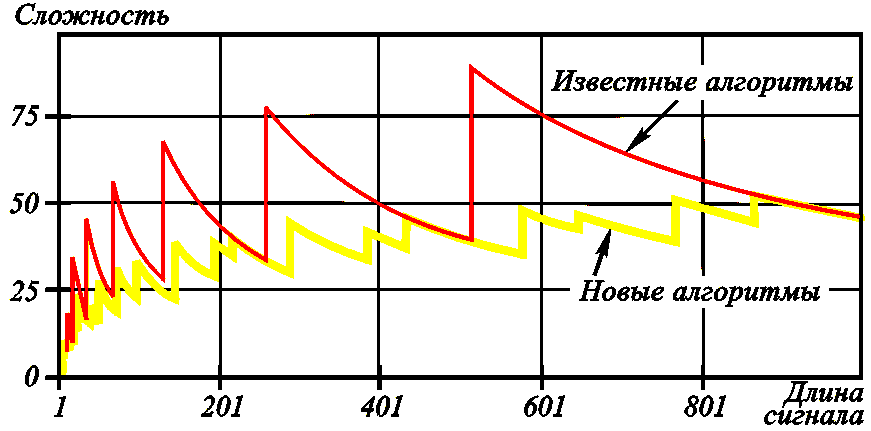
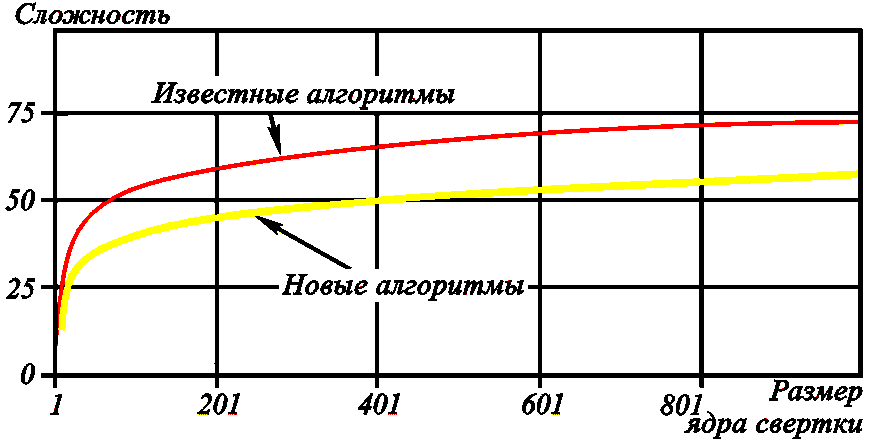
Алгоритмы свертки
основаны на использовании:
а) новых алгоритмов ДПФ и оптимальном секционировании,
б) параллельно-рекурсивного вычисления сверток при полиномиальной аппроксимации
импульсных характеристик (ядра свертки).
 |
 |
|
Сверхбыстрые
алгоритмы
спектральных преобразований |
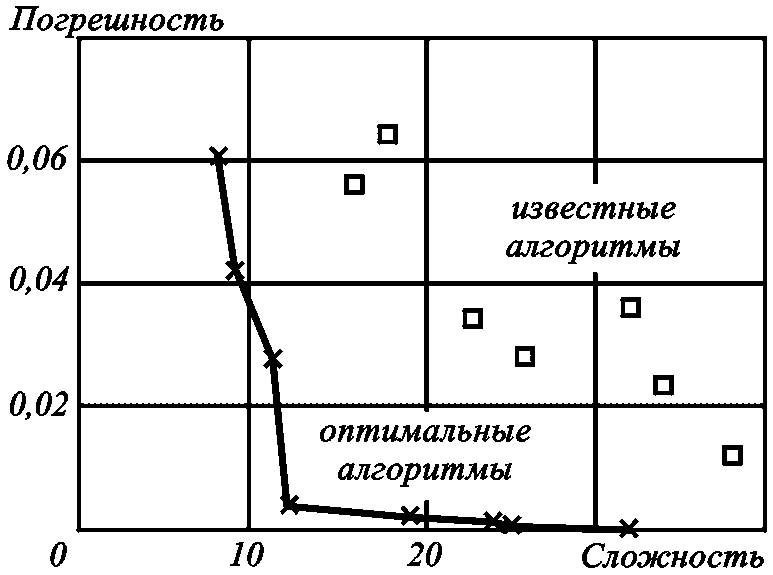
Оптимальное
селекционирование свертки |
Параллельно-рекурсивная реализация свертки
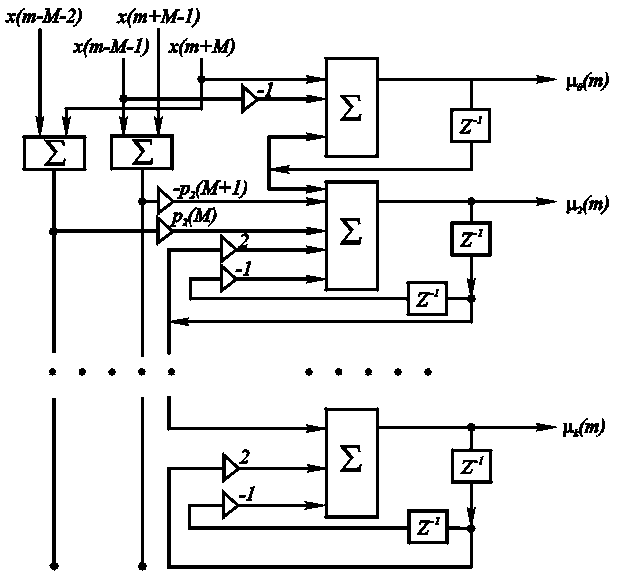
 |
 |
|
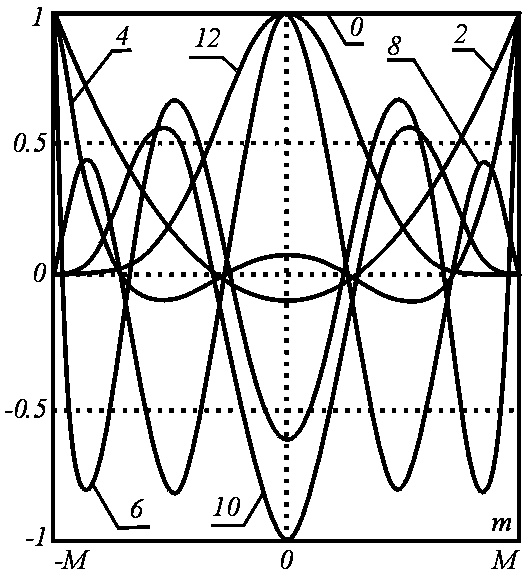
Полиномиальные
базисы
|
Пример:
выбор алгоритмов
свертки с Гауссовским ядром |
Публикации:
1. Proc. of the 7th Intern. Conf. on Comp. Analysis of Images and Pattern,
Springer. - LNCS 1296. - P.621-628.
2. Pattern Recognition and Image Analysis. - 1998. - v.8. - №3. - P.347-349.